Voor het tekenen van grafieken van
functies zijn de
volgende stappen nodig.
Nadat een functie b.v.
f(x)=(sin(x))
is ingevoerd:
1) Klik op grafiek.
Er verschijnt
nu een nieuw venster waarin de gegevens
voor de
grafiek moeten worden ingevoerd.
2) Voer een ondergrens en een
bovengrens in.
3) Voer het aantal stappen (punten) in. Bij voorbeeld 40.
4) Klik op de checkbox rechts. Er
verschijnt nu een
nieuwe knop Tabel.
5) Klik op Tabel.
Als deze knop verdwijnt is de tabel voor de grafiek klaar.
6) De grafiek wordt automatisch
getekend.
Op deze wijze kunnen 3 grafieken tegelijk worden
getekend nl. voor de tabellen f,
g en h.

f(x,y)=(sin(x)+sin(y)+z) z=1
g(x,y)=(cos(x)-sin(y)+z) z=1
Bovenstaande 2grafieken leveren m.b.v
Query onderstaande
grafiek., f(x,y) tegen g(x,y) op.
f(x,y) tegen g(x,y) in het x-y vlak.
M.b.v.
de schuifbalk kan de stand van het x-y vlak
t.o.v. de Z-As gevariëerd worden. M.b.v. de
instelknoppen kan de Zoom resp. de Shift langs de 3 assen ingesteld
worden.
Wanneer op de grafiek geklikt wordt verschijnen de X, Y,
Z
coördinaten boven in het grafiekenvenster. Hiervoor kan men
het beste
de grafiek tekenen met punten i.p.v.
met een doorgetrokken lijn (Zie Instellingen->3Dgrafieken).
I.p.v. de
tabelwaarden kunnen ook de grafische (pixel) coördinaten
weergegeven worden.
Dit is instelbaar via Instellingen->3Dgrafieken. Wanneer een
formule
beschikbaar is worden de coördinaten berekend. Dit gaat
automatisch.
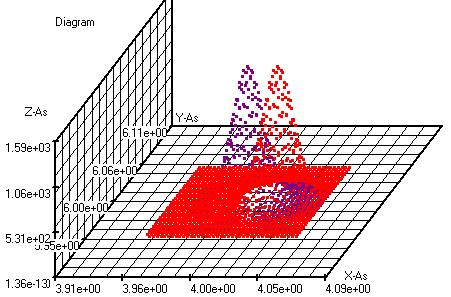
f(x,y)=((5000/pi)*exp(-5000*(
(x-4)^2+(y-6)^2)))
g(x,y)=((5000/pi)*exp(-5000*(
(x-4.02)^2+(y-6)^2)))
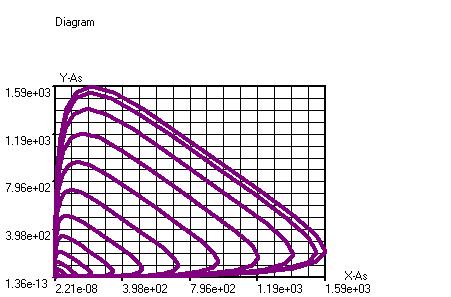
f(x,y) tegen g(x,y)
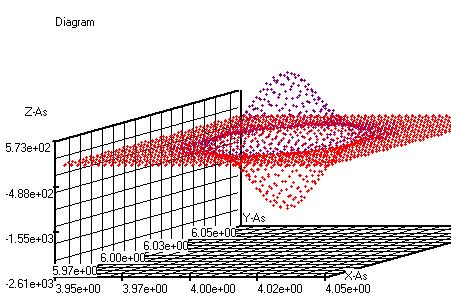
g(x,y)=((-5000/pi)*exp(-5000*(
(x-4)^2+(y-6)^2))) (rood)
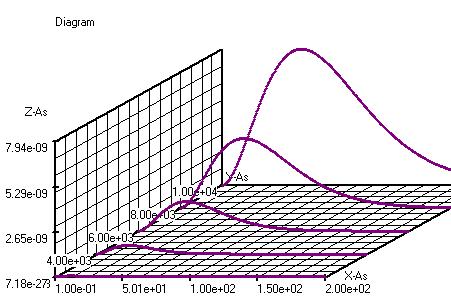
f(f,T)=((6.1677E-13*((f)^3))/(
exp( (4.7979E2*(f))/(T))-1))
Grafieken
in het
complexe vlak.
Functies van een complexe variabele
kan men tekenen in
het 3-Dim grafieken venster.
De complexe variabele moet men dan
splitsen in een reëel
deel en een imaginair deel.
B.v. f(z)= sin(z) : z=x+j*y is complex, wordt alsvolgt
ingevoerd: f(x,y)=sin(x’y) (Let op
het accent (x’y)
aan de
bovenkant). Nu is
f(x,y) een complexe
functie van de 2 reële
variabelen x en
y, waarbij x het
reële deel voorstelt
en y het imaginaire deel. Hierbij moet het variabelenvenster
op “Var”
ingesteld worden en dus niet op “Z”.
Zie complexe getallen voor het invoeren van een complex getal. De
waarde
van f(x,y) wordt
als een complex getal
opgeslagen. Óf de absolute waarde óf het argument
van f(x,y) wordt uitgezet in
het complexe vlak; dit is in te stellen onder “Instellingen à Algemeen”.
1e
methode
Met behulp van Structured Query Langage (SQL) kan men kolommen uit verschillende tabellen samenvoegen tot een nieuwe tabel. Onder de menu optie Tabellen->Query kan men hiervoor een SQL opdrachtregel invoeren.
(hoeken instellen op radialen in het hoofdmenu onder Instellingen/Algemeen.)
g(t)=(t+2*cos(5*t))
M.b.v. Naar 3DIM->Aan stuurt men de tabel naar het 3DIM grafieken venster.
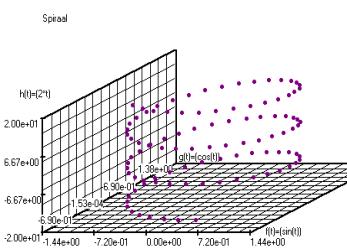
Toepassing
van SQL : Spiraal
f(t)=(sin(t))
g(t)=(cos(t))
h(t)=(2*t)
Aantal Stappen :
100 ; t :
-10 10
; Hoeken in
radialen.
SQL Opdracht:
select f_nr, f_functie, g_functie, h_functie from f_tabel.dbf, g_tabel.dbf, h_tabel.dbf where f_nr = g_nr and g_nr=h_nr;
2e
methode
M.b.v. de menu optie Modellen kunnen
grafieken getekend
worden op grond van parametrische vergelijkingen.
Voorbeeld
Programma
Startwaarden
t=t+dt
t=0
x=sin(2*(t))+0.5
dt=0.1
y=1.3*cos(t)+0.5
x=0.5
y=1.8
Opm. hoeken instellen op radialen in het hoofdmenu onder
Instellingen/Algemeen.
Matrix gegevens kunnen alleen in het matrixvenster
worden
ingevoerd.
Het
matrix venster komt te voorschijn als op de knop matrix
wordt
geklikt. Deze knop zit naast de knop grafiek.
In
het matrixvenster staat aangegeven hoe matrixgegevens
moeten
worden ingevoerd.
Bijvoorbeeld
bewerkingen op een matrix A( ).
Deze
bewerkingen moeten in een invoervenster worden ingevoerd.
Matrixbewerkingen
a) De inverse van matrix A( ): voer
in: A( )^-1
b) De getransponeerde van matrix A( )
: voer in A( )^ Tr
c) Transformeren van een
tridiagonaalmatrix A() naar
een diagonaalmatrix : voer in diag(A)
d) Transformeren van een symmetrische
matrix A() naar
een tridiagonaalmatrix volgens de methode
van
Householder: voer in tridiag(A).
Matrix berekeningen.
a) De som van de matrices A( ) en B( )
: voer in A( ) +
B( ) =
b) Het verschil van de matrices A( )
en B( ) : voer in
A( ) - B( ) =
c) Het product van matrix A( ) en
matrix B( ) : voer in
A( ) * B( ) =
d) De derde macht van matrix A( ) :
voer in A( )^3
e) Een kombinatie van bewerkingen en
berekeningen: b.v.
A( ) ^-1+ B( ) * C( ) ^ 3=
Matrixfuncties
Bijvoorbeeld f(x, y)=( 2*A( )^-1 + B(
)^3 ) , waarbij x
en y twee variabelen zijn die voorkomen in A() en B().
Deze variabelen moeten tussen haakjes
staan in dematrix.
De volgorde van de bewerkingen (binnen
de haakjes) is
achtereenvolgens: machtsverheffen, vermenigvuldigen, optellen,
aftrekken.
Met behulp van de volgende stappen kan de determinant bepaald worden.
1) Typ de matrix in het matrixvenster.
2) Selecteer de matrix en klik op een
matrix symbool (b.v. op
A( ) ).
3) Typ in een invoervenster det(A)= .
Eigenwaarden en
Eigenvectoren van een matrix.
De
nauwkeurigheid van de methodes is instelbaar in het
instellingen menu
m.b.v. Iteraties.
a)
eigwn(A)
: Berekent alle eigenwaarden
en eigenvectoren van een matrix A(). De methode wordt
automatisch gekozen. Voor symmetrische matrices: QR
Methode; voor
niet-symmetrische
matrices: Inverse Power Methode
b)
eigwd(A)
: Berekent de dominante
eigenwaarde van een matrix A() volgens de Power Methode.
c)
eigwds(A)
: Berekent de dominante
eigenwaarde van een symmetrische matrix A() volgens de
Symmetrische Power
Methode met
minder iteraties dan bij b).
d) eigwq(A, q)
: Berekent een benaderende eigenwaarde en
eigenvector
van een matrix A() in de buurt
van het getal q
volgens de Inverse Power Methode. Nogmaals deze bewerking uitvoeren
met als q de
gevonden eigenwaarde
levert
een nauwkeurigere eigenwaarde op.
Opm.de maximale
matrixgrootte in dit programma is een 9
maal 9 matrix.
Bij het sommeren over een
functie doorloopt de functie variabele
een reeks gehele getallen
vanaf een beginwaarde t/m een eindwaarde.
Met behulp van de
volgende opdrachten kan over een functie gesommeerd worden.
a)
Voor een functie f(x) : typ in
somf(x:a,b)=
Hierin is a: ondergrens.
Hierin
is b: bovengrens.
b) Voor
een functie g(x) : typ in somg(x:a,b)=
Hierin
is a: ondergrens.
Hierin
is b: bovengrens.
c) Voor een functie h(x) : typ in
somh(x:a,b)=
Hierin
is a: ondergrens.
Hierin
is b: bovengrens.
1) Wanneer een tabel voor
een grafiek gemaakt wordt verschijnt
de waarde van de integraal automatisch in Uit1.
2) Door de volgende opdracht in te typen
in een invoervenster:
a) Voor een functie f(x) : typ
in intf(x:a,b)=
Hierin
is a: ondergrens.
Hierin
is b: bovengrens.
b) Voor een functie g(x) : typ
in intg(x:a,b)=
Hierin
is a: ondergrens.
Hierin
is b: bovengrens.
c) Voor
een functie h(x) : typ
in inth(x:a,b)=
Hierin
is a: ondergrens.
Hierin
is b: bovengrens.
Dubbel en tripel integralen kunnen zowel met vaste
grenzen als met variabele
grenzen ingevoerd worden.
.De
volgorde van integreren wordt
hierbij bepaald door de volgorde van de variabelen in
het varvenster.
In
onderstaande voorbeeeld is deze
volgorde van boven naar beneden: y, x .(Zie ook het
voorbeeld bij tripel
integralen)
De volgorde van de variabelen
in het grafiekvenster is niet van belang.

Voer in : f(x,y)=( (x) * (y)^2
)
Integratie grenzen: x van 2.1 – 2.5 ; Ondergrens 2.1 ,
Bovengrens2.5.
y van 1.2
– 1.4 ;
Ondergrens 1.2
, Bovengrens
1.4.
Aantal stappen voor x en y is 4 .
Integratie methode instellen op
Composite Simpson. (Zie Hoofdmenu :
Instellingen)
Voorbeeld
van een tripelintegraal
Integratie methode instellen
opGauss. (Zie
Hoofdmenu : Instellingen)
Hoeken instellen op
radialen. 2*pi= 6.283185
(Integraal van f(x,y,z) over
een bolschil m.b.v. bolcoördinaten)
![]()
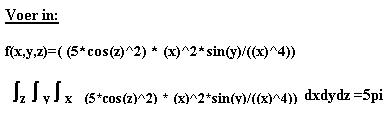
Aantal stappen voor x en y en z
is 6.
Integratie grenzen: x van 1 – 2 ;
Ondergrens 1
, Bovengrens2
y van 0
– pi ; Ondergrens 0,
Bovengrens pi.
z van
0 -- 6.283185
;
Ondergrens
0, Bovengrens
2pi.
In het kladblok
verschijnt:
intf(
x :1.000000,2.000000; y :0.000000,3.141593; z :0.000000,6.283185) 15.685618700000 Termen: 216
Integreren
met variabele grenzen.
In
het invoervenster grafiek
kunnen bij ondergrens en bovengrens ook variabele grenzen in
formulevorm
ingevuld worden. De volgorde van integreren wordt hierbij bepaald door de
volgorde van de variabelen in het varvenster.
In
onderstaande voorbeeeld is deze
volgorde van boven naar beneden: z, y, x. Zie varvenster.
De volgorde van de variabelen
in het grafiekvenster is niet van belang.

Varvenster
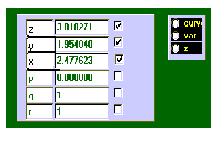
Voer
in : f(x,y,z)=( 1/(y) * sin( (z) / (y) ) )
Integratie grenzen: x van 0 - p ;
Ondergrens 0
, Bovengrens
(3.1415926
). Let op de haakjes!
y van 0
– x ; Ondergrens 0 ,
Bovengrens (x)
.
z van 0
– xy ; Ondergrens 0 ,
Bovengrens ((x)*(y))
.
Grafiekvenster
Aantal stappen voor x, y en
z is 2.
Integratie methode instellen op
Gauss. (Zie Hoofdmenu : Instellingen)
Hoeken
op Rad instellen.
Integreren
van functies van complexe
variabelen.
z is complex.
Voorbeeld
f(z)=( (z)^2)
Ondergrens is : (0,0)
Bovengrens is : (1,1)
Aantal stappen is : 40
In het kladblok
verschijnt:
intf( z :0.000000,1.000000) + j
* intf( z :0.000000,1.000000)
(-0.666667, 0.666667) Termen: 82
Uitkomst is : (-0.666667,
0.666667)
f(z)=cos(z)
pi= (3.141593, 0.000000)
Ondergrens is : (0, -3.141593)
Bovengrens is : (0,
3.141593)
Aantal stappen is : 40
In het kladblok
verschijnt:
intf( z :0.000000,0.000000) + j
* intf( z :-3.141593,3.141593)
(0.000000, 23.097563) Termen: 42
Uitkomst is : (0.000000,
23.097563)
De integratie van een functie van een
complexe variabele z
langs een contour z(t) in het complexe vlak.
De complexe variabele en de contour
moeten in het
instellingen menu ingevoerd worden.
Tevens moet de afgeleide z’
van z naar de
parameter t in het venster dz in het instellingen
menu ingevoerd
worden.
De boven en ondergrens van de
parameter t moeten
in het grafiek venster ingesteld
worden.
Voorbeeld:
f(z)=e^z /(z-2)
Voer in : f(z)=(exp(z)/(z-2))
In het kladblok verschijnt:
f(z)=(exp(z)/((z)-2))
(20.085537, 0.000000)
z= (1.0,1.0)
In het instellingenmenu:
Contour
= (p) +
(r)*exp((j)*(t))
z’= j*(r)*exp((j)*(t))
(De contour is een circel om het punt p)
In het variabelen venster (z) : p=(2,0)
r=(1,0)
In het grafiekvenster parameter t,: Ondergrens (0,0) , Bovengrens: (6.283185,0)
In het kladblok verschijnt:
intf( t
:0.000000,6.283185) +
j * intf( t :0.000000,0.000000)
(-0.000002, 46.426802) Termen: 42
Uitkomst is : (-0.000002, 46.426802)
Voorbeeld:
f(z)=(z-p)^m

Voer in: f(z)=((z-p)^m) , z= (1.0,1.0) p= (2.0,0.0) m= (5,0)
In het kladblok verschijnt:
f(z)=(((z)-(p))^(m)) (1.000000, 0.000000) z= (1.0,1.0) p= (2.0,0.0) m= (5,0)
In het
instellingenmenu:
Contour
= (p) +
(r)*exp((j)*(t))
z’= j*(r)*exp((j)*(t))
(De contour is een circel om het punt p)
Integratiegrenzen voor de parameter t, in het grafiekvenster : Ondergrens (0,0) , Bovengrens: (6.283185, 0)
Met r= (1.0,0.0) en m=(5,0) in het variabelenvenster:
In het kladblok verschijnt:
intf( t
:0.000000,6.283185) +
j * intf( t :0.000000,0.000000)
(0.000004, 0.000001) Termen: 42
Uitkomst is : (0.000004,
0.000001)
met m=(-1,0) :
In het kladblok verschijnt:
intf( t
:0.000000,6.283185) +
j * intf( t :0.000000,0.000000)
(0.000000, 6.283185) Termen: 42
Uitkomst is : (0.000000, 6.283185)
Opm.:
Dit
werkt alleen met de functiesymbolen f, g, h en met niet
geïndiceerde
variabelen.
Met behulp van de volgende opdracht kan een functie b.v. f(x) gedifferentieerd worden.
a) Bepaling van de eerste afgeleide
functie van f(x).
Typ in een invoervenster:
g(x)=(difxf(x))
Lees
dit als “Differentieer (dif)
naar x (x)
de functie f(x)”.
b) Bepaling van de tweede afgeleide
functie van f(x).
Typ in een invoervenster:
h(x)=(difxxf(x)
Lees
dit als “Differentieer (dif)
tweemaal naar x (xx) de functie f(x)”.
Opm. de stapgrootte h voor het differentiëren is instelbaar.
Nu kunnen tegelijkertijd f(x),
g(x) en h(x) getekend worden, nadat van f(x), g(x) en h(x) eerst
een tabel gemaakt is. De
tabelinstellingen moeten hierbij voor de drie functies hetzelfde zijn.
Onder het var(iabelen) menu zit het invoervenster voor curve fitting.
Curve fitting bepaalt van een reeks getallenparen de bijbehorende polynoom functie.
Met
behulp van curve fitting kan
ook geïnterpoleerd en geëxtrapoleerd
worden.
De volgende stappen zijn
noodzakelijk.
1) Maak een tabel met de meetpunten.Dit kan op twee manieren.
a) Op een diskette (a:drive).
Dit bestand moet het volgende formaat hebben:
Typ
op de eerste regel:
x
y
Zet vervolgens onder x de x-waarden en onder y de y-waarden
gescheiden
door spaties.
b) Met behulp van de
tabellen f, g of h .
Deze tabellen zijn te vinden in het hoofdmenu onder de knop tabellen.
Vul vervolgens zo´n tabel in.
2) Klik het
aantal konstanten aan (C0, C1, C2 etc.) waarmee de polynoom gevormd
moet
worden.
3) Klik op de knop
start.
Opm. de polynoom
functie verschijnt in
invoervenster1.
Niet lineaire
vergelijkingen met èèn
onbekende.
De
functie solve( ) lost een niet lineaire
vergelijking op volgens de
Muller-methode.
Voorbeeld:
(x)^3 - 2*(x)^2 - 5 = 0
Voer in : f(x)=(
(x)^3-2*(x)^2-5)
Opm.:
Dit werkt alleen met de functiesymbolen f, g, h en met niet
geïndiceerde
variabelen.
(Zoek een benadering van
het nulpunt in de buurt van het punt x=2.0)
Voer in: solve(f, 2.0) =
.
Of maak eerst een
grafiek van de functie f(x)=( (x)^3-2*(x)^2-5) en klik een punt in de
buurt van
f(x)=0 aan.
Druk vervolgens op de
knop Y=0
.
In het kladblok
verschijnt:
Iteraties Muller-methode:
5
Nulpunt benadering:
solve(f, 2)= 2.690647
x= 2.690647
x= 2.690647
is de voorlaatste benadering.
Niet lineaire
vergelijkingen met een
complexe oplossing.
De functie f(x)=(
16*(x)^4-40*(x)^3+5*(x)^2+20*(x)+6)
=0
heeft twee reële en een complexe oplossing.
Voer in: f(x)=(
16*(x)^4-40*(x)^3+5*(x)^2+20*(x)+6)
Opm.:
Dit werkt alleen met de functiesymbolen f, g, h en met niet
geïndiceerde
variabelen.
Vervolgens: solve(f, 2) =
.
In het kladblok
verschijnt:
Iteraties Muller-methode:
4
Nulpunt benadering:
solve(f, 2)= 1.970446
x= 1.970446
Voer in: solve(f, 1) = .
In het kladblok
verschijnt:
Iteraties Muller-methode:
5
Nulpunt benadering:
solve(f, 1)= 1.241677
x= 1.241678
Voer in: solve(f, 0) = .
In het kladblok
verschijnt:
Deze benadering levert
geen reële oplossing op.
Klik op z en voer de
functie als een complexe functie in,
voor een complexe
oplossing.
Benaderende oplossing:
solve(f, 0)=
(-0.356062, 0.162759)
x= (-0.356061, 0.162758)
Stelsel niet lineaire
vergelijkingen
Er zijn twee manieren om
een oplossing te vinden .
Methode 1 zoekt eerst een
benaderende oplossing .
Methode 1:
Selecteer met de
muis het voorbeeld
in het
vectorvenster.
Klik vervolgens op S.
Hoeken instellen opRad in
het Instellingenmenu.
Vx=(3*(x)-cos((y)*(z))-0.5)
Vy=((x)^2-81*((y)+0.1)^2+sin(z)+1.06)
Vz=(exp(-(x)*(y))+20*(z)+(10*pi-3)/3)
f1(x,y,z)=(difxg(x,y,z))
f1(x,y,z)=(difyg(x,y,z))
f1(x,y,z)=(difzg(x,y,z))
*
*
* * *
*
Iteraties
SteepDescent-methode: 3
Benaderende oplossing.
x = 1.122011e-02
y = 1.009712e-02
z = -5.228119e-01
* *
* * *
* *
* * *
* * *
*
* * *
* * *
*
* * *
* *
* * *
* * *
*
* * *
* *
* *
* *
Iteraties
Newton-methode: 5
x = 5.000000e-01
y = 4.339851e-10
z = -5.235988e-01
Methode 2:
Selecteer met de
muis het voorbeeld
in het vectorvenster
en klik een vector symbool aan, b.v.V1().
Met behulp van de
functie solven(....) kan een benaderende
oplossing opgegeven
worden.
B.v.:
solven(V1(1,1,1))=
Hoeken instellen opRad in
het Instellingenmenu.
Vx=(3*(x)-cos((y)*(z))-0.5)
Vy=((x)^2-81*((y)+0.1)^2+sin(z)+1.06)
Vz=(exp(-(x)*(y))+20*(z)+(10*pi-3)/3)
f1(x,y,z)=(difxf(x,y,z))
f1(x,y,z)=(difyf(x,y,z))
f1(x,y,z)=(difzf(x,y,z))
*
*
* * *
* *
* * *
* * *
*
* * *
* *
* * *
*
* * *
* *
* * *
* * *
*
* * *
* * *
Iteraties
Newton-methode: 5
x = 5.000000e-01
y = 4.507480e-10
z = -5.235988e-01
solven(V1(1,1,1))=
0.000000
x= 0.500000
y=
0.000000 z=
-0.523599 N=
1.0 h=
1.0
Stelsel lineaire
vergelijkingen
In het matrixvenster staat
aangegeven hoe een stelsel lineaire vergelijkingen moet worden
ingevoerd.
Het aantal onbekenden is
maximaal 6.
Door op de knop ” stelsel “ te
klikken wordt het stelsel opgelost.
De oplossing verschijnt
onderaan in het matrixvenster.
Beginwaarde problemen
(Initial value probems).
Methode van Euler.
Voorbeeld:
Typ
in f(x)=(y-x^2+1) vervolgens
euler(f(y0:0.5))=.
f(x)=(y-x^2+1)
is identiek met dy/dx=y-x^2+1 .
d? geeft aan dat
in het grafiekvenster
een variabele met begin en eindwaarden moet
worden ingevoerd.
In dit geval is deze
variabele x. Als
begin waarde van x
kiezen we 0 en als eindwaarde 2.Voor het aantal stappen kiezen we 10.
De beginwaarde van de
oplossing is :
y0=0. 5. In tabel h
verschijnen de volgende waarden voor y en x.
0.5 0
0.8 0.2
1. 092
0.4
1.36 0.6
1.588 0.8
1.76
1.0
1.86 1.2
1.872 1.4
1.78 1.6
1.568 1.8
1.22
2.0
Runge-Kutta methode.
(RK4)
Voorbeeld:
Typ in
f(x)=(y-x^2+1) en
vervolgens rungek(f(y0:0.5))=
.
Verder kiezen we dezelfde
instellingen als bij de methode van Euler.
Runge-Kutta-Fehlberg
methode (RK45-methode).
Voorbeeld:
Typ in
f(x)=(y-x^2+1) en
vervolgens rungekf(f(y0:0.5))=.
Verder kiezen we dezelfde
instellingen als bij de methode van Euler.
Stelsel Differentiaalvergelijkingen
De
hierbij gebruikte methode
is: Runge-Kutta methode (RK4)
of
(RKF) zonder variabele stapgrootte.
De
algemene opdracht voor de RK-methode luidt: rungeks(f1,f2,...,fn(Y1:...,Y2:...,....,Yn:...))=
Of
voor de RkF-methode: rungekfs(f1,f2,...,fn(Y1:...,Y2:...,.....,Yn:...))=
De instellingen voor de
RKF-methode vinden plaats onder de menu optie
differentiaalvergelijkingen onder
instellingen op het hoofdmenu.
Voorbeeld
1
Een stelsel van twee
differentiaalvergelijkingen, n=2.
Typ in
f1(t,Y1,Y2)=(-4*(Y1)+3*(Y2)+6)
f2(t,Y1,Y2)=(-2.4*(Y1)+1.6*(Y2)+3.6)
De beginwaarden zijn voor
Y1: 0 en voor Y2:0.
en vervolgens
rungeks(f1,f2(Y1: 0,Y2:0)=
De integratie variabele
is t. Als begin waarde van t kiezen we 0 en als eindwaarde 0.5.
Voor het aantal stappen
kiezen we 5.
Tabel letter is
instelbaar. (Zie Instellingen->Oplossingstabel
Differentiaalvergelijkingen)
In tabellen verschijnen
de waarden voor Y1 en Y2. Onder Functie staat Y1 en
onder Y staat
Y2.
In het grafiekvenster
verschijnen de grafieken.
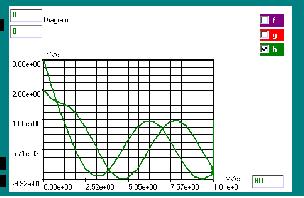
Voorbeeld
2
n=2.
Typ in
f1(x,Y1,Y2)=(-2*(Y1)+
(Y2)+2*sin(x))
f2(x,Y1,Y2)=((Y1)-2*(Y2)+2*(cos(x)-sin(x)))
en vervolgens
rungeks(f1,f2(Y1:2,Y2:3)=
De beginwaarden zijn voor
Y1:2 en voor Y2:3.
De integratie variabele
is x. Als begin waarde van x kiezen we 0 en als eindwaarde 10.
Voor het aantal stappen
kiezen we 60. Hoek x in radialen instellen.
In het grafiekvenster
verschijnt de volgende oplossing voor Y1 en Y2.
Expliciete
methodes m.b.v. Butcher coefficienten
Onder
InstellingenàDifferentiaalvergelijkingenàButcher Matrix
kan men voor een expliciete Runge-Kutta
methode de Butcher coefficienten invullen.
De
bijbehorende opdrachtregel
luidt: rksbutcher(f1,f2,...,fn(Y1:...,Y2:...,....,Yn:...))=
De
instellingen gebeuren op
dezelfde wijze als voor de hier boven beschreven RK-methodes.
M.b.v.
de knoppen f, g,
h onder
grafiekinstellingen kan men de
tabel kiezen voor het opslaan van de oplossing.
Invoer van vectoren. (zie
vectorvenster)
Nadat
een vector is ingevoerd kunnen op de vector bewerkingen worden
uitgevoerd.
Bijvoorbeeld
bewerkingen op een vector V1()
Deze
bewerkingen moeten in een invoervenster worden ingevoerd.
Vector berekeningen.
a) De som van de
vectoren V1 en V2: voer in V1()
+ V2()=
b) Het verschil van de
vectoren V1 en V2: voer in V1()
-V2()=
c) Het inproduct van de
vectoren V1 en V2: voer in V1()
. V2()=
d) Het uitproduct van
de vectoren V1 en V2: voer in V1() * V2()=
e) De Jacobiaan van
een stelsel vergelijkingen : voer in jac(V1())=
Opm. Bij berekeningen met vectoren
zijn ook rekenkundige
haakjes toegestaan.
De volgorde van de bewerkingen (binnen
de haakjes) is
achtereenvolgens: machtsverheffen, uitproduct, inproduct, optellen,
aftrekken.
B.v. Vector V1() bevat:
Vx=(3*(x)-cos((y)*(z))-0.5)
Vy=((x)^2-81*((y)+0.1)^2+sin(z)+1.06)
Vz=(exp(-(x)*(y))+20*(z)+(10*pi-3)/3)
Voer in :
f(x,y,z)=(V1(x,y,z)), vervolgens kunnnen m.b.v. f(.., ..,
..)= voor elke
waarde van x, resp y en z de
vectorcomponenten worden uitgerekend.
Voorbeeld Jacobiaan matrix:
Bereken de Jacobiaan van het voorbeeld
stelsel in het
vectorvenster in het punt x=1,
y=1,
z=1.
Voer eerst in het variabelen venster
de coordinaten x=1,
y=1, z=1 in.
Selecteer in het vector venster het
voorbeeld stelsel
vergelijkingen en klik op V1.
Voer vervolgens in jac(V1()) = of jac(V1(1,1,1)) =
Hoeken
instellen opRad in het Instellingenmenu.
In het kladblok verschijnt:
Vector
V1
Vx=(3*(x)-cos((y)*(z))-0.5)
Vy=((x)^2-81*((y)+0.1)^2+sin(z)+1.06)
Vz=(exp(-(x)*(y))+20*(z)+(10*pi-3)/3)
f1(x,y,z)=(difxf(x,y,z))
f1(x,y,z)=(difyf(x,y,z))
f1(x,y,z)=(difzf(x,y,z))
f1(x,y,z)=(difxf(x,y,z))
f1(x,y,z)=(difyf(x,y,z))
f1(x,y,z)=(difzf(x,y,z))
f1(x,y,z)=(difxf(x,y,z))
f1(x,y,z)=(difyf(x,y,z))
f1(x,y,z)=(difzf(x,y,z))
Jac(V1())= Matrix U
x= 1.000000
y= 1.000000
z= 1.000000
N= 1.0
h= 1.0
Matrix U (Uitvoer)
(3 ,
0.816573 , 0.816573
)
(2 ,
-178.2 , 0.524316
)
(-0.354069 , -0.354069 , 20 )
Vectorvelden
a) Divergentie van
een vectorveld in een punt x, y ,z
:
voer in div(V1())=
b) Rotatie van een
vectorveld in een punt x, y, z
:
voer in rot(V1())=
c) Gradient van een
functie f in een
punt x, y, z
: voer in grad(f(x,y,z))=
Berekening van een gradient.
Opm.: Dit werkt alleen met de
functiesymbolen f, g,
h en met niet geïndiceerde variabelen.
Voer in:
f(x,y,z)=(3*(x)-cos((y)*(z))-0.5)
Hoeken
instellen opRad in het Instellingenmenu.
In het kladblok verschijnt:
f1(x,y,z)=(difyf(x,y,z))
f1(x,y,z)=(difzf(x,y,z))
grad(f(1,2,3))= Matrix U
x= 1.000000
y= 2.000000
z= 3.000000
h= 1.
Matrix U (Uitvoer)
(3 )
(-0.065587 )
(-0.374006 )
Berekeningen met
Complexe getallen

In het venster (z)
voor complexe variabelen in de vorm (a,
b).
Standaardfuncties met
complexe getallen.
![]()
arg(z)
imag(z)
real(z)
abs(z)
sin(z)
sinh(z)
asin(z)
cos(z)
cosh(z)
acos(z)
tan(z)
tanh(z)
atan(z)
exp(z)
log(z)
ln(z)
sqrt(z)
Algemeen
abs(x)
pi
sqrt(x)
(n)!
(n,m)! = n! / m(n-m)!
Trigonometrische
Formules
Voor alle hoeken
geldt: x in radialen of
in graden (Zie Instellingen in het hoofdmenu)
asin(x)
sinh(x)
asinh(x)
cos(x)
acos(x)
cosh(x)
acosh(x)
tan(x)
atan(x)
tanh(x)
atanh(x)
Sa(x) :
Sa(x)=sin(x)/x
exp(x)
log(x)
ln(x)
Een voorbeeld van een integraal functie is Si(x).
Si(x) is de integraal van 0 t/m x van de functie sin(x)/(x).
Sa(x)=(sin(x)/(x)) is de zogenaamde sample functie. Om onderstaande grafiek te verkrijgen moet men invoeren : f(x,y)=(int(Sa(x))), samen met de onderstaande instellingen. Hoeken instellen op radialen. Si(x) convergeert naar ± п/2.
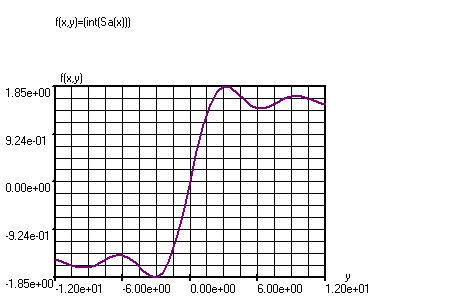
Grafiek venster:
Variabele Stappen Ondergrens Bovengrens
x
40
0
(y)
y
40
-12
12
Opm. : In het varvenster moet x boven y staan ; x is de hulp variabele, x loopt telkens van 0 t/m y.
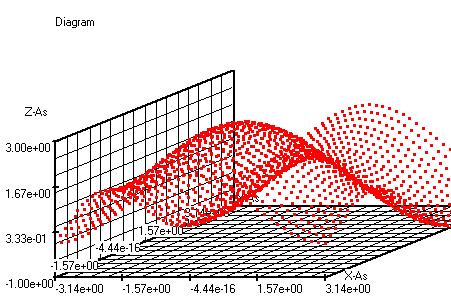
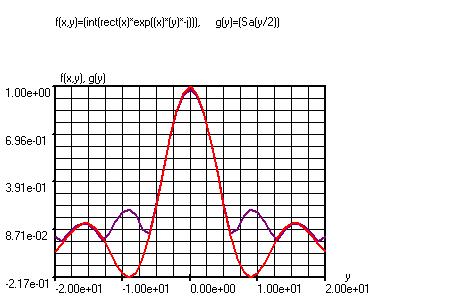
f(x,y)=(int(rect(x)*exp((x)*(y)*-j)))
Deze functie berekent de Fourier integraal van de rechthoekige puls rect(x) met amplitude 1.
Variabele Stappen Ondergrens Bovengrens
x 20 0 1
y 40 -20 20
Opm. : In het varvenster moet x boven y staan ; x is de hulp variabele, x loopt telkens van 0 t/m y. In het diagram is de absolute waarde van de complexe uitkomst f(x,y) weergegeven.
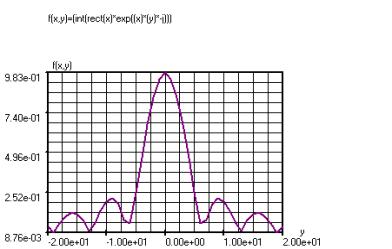
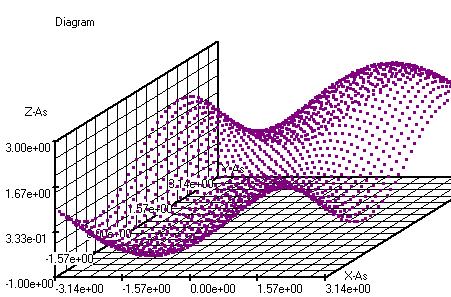
In onderstaande diagram
is de analoge oplossing ( g(y)=(Sa(y/2)), hoeken in
radialen ) van de
Fourier integraal van rect(x) uitgezet samen met de numerieke oplossing
f(x,y).
Paars:
f(x,y).
Rood :
g(y)
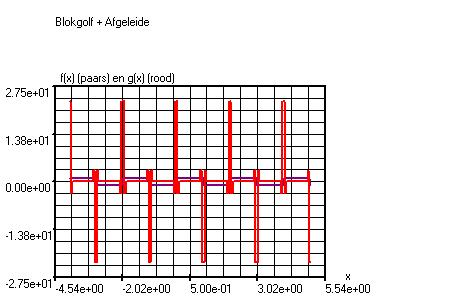
Periodieke Functies (Blokgolf en
Zaagtand)
Onder
Instellingen->Periodieke functies kan men voor een blokgolf rect(x)
en een zaagtand tri(x) m.b.v. T1 en T2 de
pulsduur instellen. Shift
verschuift het beginpunt van de grafiek t.o.v. de oorsprong.
Voorbeeld
f(x)=(2*rect(x)-1) (Blokgolf)
g(x)=(difxf(x)) (Afgeleide van de blokgolf)
g(x)=((f(((x)-2*(h)))+$(((x)+2*(h)))-8*f(((x)-(h)))+$(((x)+(h)))+8*f(((x)+(h)))+$(((x)-(h)))-f(((x)+2*(h)))+$(((x)-2*(h))))/(12*(h)))
Grafiekvenster
x:
-4.0 – 5.0
Stappen:
400
h=0.05
Instellingen->Periodieke
functies
T1=1.0
T2=1.0
Shift=-4.0
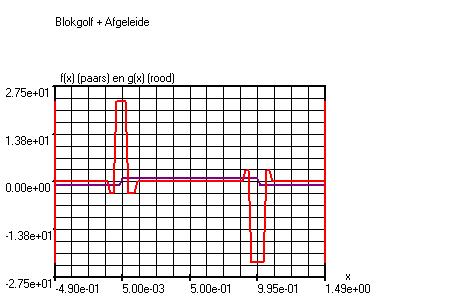
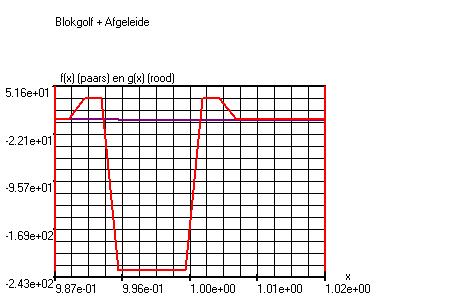
Grafiekvenster
x:
-4.0 – 5.0
Stappen:
4000
Variabelenvenster
h=0.005
Instellingen->Periodieke
functies
T1=1.0
T2=1.0
Shift=-4.0
Voorbeeld 1
De primitieve van sin(x) is -cos(x) + Constante
Met behulp van de opdrachtregel f(x,y)=(int(sin(y))), waarbij y de hulp variabele is kan men van sin(x) de Grafiek en Tabel van de Primitieve van sin(x) berekenen.
Paars : f(x,y)=(int(sin(y)))
Stappen Ondergrens
Bovengrens
x : 40 -pi +pi
y : 40 -1.570796 (x)
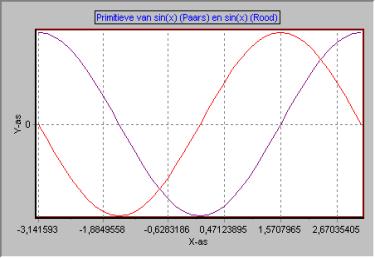
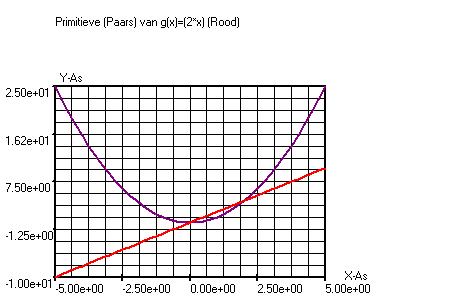
Voorbeeld 2
De Primitieve van f(x)=(2*(x)) voert men als volgt in:
f(x,y)=(int(2*(y)),. y is de hulpvariabele.
Stappen Ondergrens Bovengrens
y :
40
0
(x)
x :
40
-5.0
+5.0